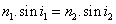ĐỀ MỤC
I.1 Hiện tượng khúc xạ ánh sáng
I.2 Quy luật của hiện tượng khúc xạ ánh sáng
I.3 Chiết suất của môi trường
I.4 Ảnh của một vật được tạo bởi sự khúc xạ ánh sáng qua mặt phân cách
giữa hai môi trường
I.5 Tính thuận nghịch trong
sự truyền ánh sáng
NỘI DUNG
I.1 Hiện tượng khúc xạ ánh sáng
Bốn thế kỷ trước CN, Euclide đã biết định luật phản xạ trên mặt phẳng: góc của tia tới tạo với pháp tuyến của mặt phẳng bằng góc của tia phản xạ với chính pháp tuyến đó. Archimède (khoảng 287-212 TCN) đã chứng minh được rằng có thể tập trung toàn bộ ánh sáng tới vào tiêu điểm của gương nếu gương này có dạng parabol. Như vậy, người Hy Lạp đã biết làm chủ kỹ thuật chế tạo gương. Trên thực tế, Archimède đã thiêu rụi hạm đội La Mã đang vây hãm thành phố Syracuse bằng cách dùng các gương parabol khổng lồ tập trung ánh sáng mặt trời lên tàu địch.
Sau đó, trong nhiều thế kỉ, người ta đã lưu ý tới một sự thật khá kì quặc, nhưng lại hiển nhiên. Đặt một cái thanh vào trong bát nước thì thấy cái thanh này dường như không còn là một vật nguyên vẹn nữa, mà trông cứ như bị cắt làm đôi; sự “bẽ gãy” này là do sự khúc xạ ánh sáng đã làm cho phần bị chìm dưới nước trông cứ như không gắn với phần nằm trên mặt nước.
Ánh sáng bị khúc xạ khi nó đi ra khỏi nước đã mang lại ảo giác là các vật trong nước hình như bị gãy khúc tại mặt phân cách và các vật vừa trông được nâng lên cao hơn so với thực tế mà người ta quan sát thấy ( như hình ảnh con cá trong nước hoặc hiện tượng đáy hồ trông thì cạn nhưng khi xuống lại thấy sâu hơn ta tưởng)
Người Hy Lạp cũng đã biết đến hiện tượng khúc xạ từ rất sớm. Ngay từ thế kỷ thứ I sau CN, trong cuốn Quang học, Ptolémée đã miêu tả thí nghiệm đã từng được Euclide nhắc đến . Đặt một cái bát to lên bàn và thả xuống đáy bát một đồng tiền xu. Hãy ngồi ở một chỗ sao cho bạn không thể nhìn thấy đồng tiền xu nếu không hơi nhổm người lên. Nghĩa là đồng xu đã nằm ngoài tầm mắt của bạn. Sau đó hãy đổ nước từ từ vào trong bát. Mức nước tăng lên và, đến một lúc nào đó, bạn sẽ nhìn thấy đồng xu mà không phải nhổm người lên. Sở dĩ bạn nhìn thấy đồng xu là nhờ khúc xạ ánh sáng: không có nước, các tia sáng xuất phát từ đồng xu không đi vào mắt; có nước, tia sáng bị lệch về phía đáy và đi vào mắt nên bạn có thể nhìn thấy nó.
Dưới đây là video minh họa cho thí nghiệm này:
Sau đó, nhà bác học Arập Alhazen đã đưa ra một lý thuyết về khúc xạ ánh sáng vào năm 1000, nhưng không phải bằng ngôn ngữ toán học. Cho đến năm 1621, Nhà vật lí Willebrord Snell (Hà Lan) đã khám phá ra định luật của sự khúc xạ ánh sang nhưng ông không công bố khám phá của mình bởi do tâm trạng chán ngán vì Snell chưa bao giờ phát hiện được nguyên nhân cho hiệu ứng khúc xạ này. Và vào năm 1637, René Descartes (Pháp) cũng đã tìm ra quy luật của sự khúc xạ và công bố những khám phá của ông về định luật phản xạ và khúc xạ. Ông đã phát hiện ra định luật khúc xạ Snell một cách độc lập, nhưng là người đầu tiên công bố nó. Bởi thế, định luật khúc xạ còn gọi là định luật Snen- Đề-các.
 |
| Snell |
Khi ánh sáng đi qua mặt phân cách giữa hai môi trường truyền sáng, thì một trong hai hiện tượng sẽ xảy ra: hoặc là nó nảy trên bề mặt của vật để quay lại phía sau, và người ta nói ánh sáng bị phản xạ (chẳng hạn, khi bạn nhìn mình trong gương, thì chính ánh sáng của cơ thể bạn được phản xạ bởi gương đi vào trong mắt bạn); hoặc là ánh sáng đi vào môi trường mới trong suốt bằng cách thay đổi hướng, và người ta nói ánh sáng bị khúc xạ. Như vậy, khúc xạ là hiện tượng chùm tia sáng bị đổi phương đột ngột khi đi qua mặt phân cách hai môi trường truyền ánh sáng.Định nghĩa khúc xạ ánh sáng là một định nghĩa về hiện tượng và các em học sinh có thể bắt gặp nhiều về hiện tượng này trong cuộc sống.
Tuy nhiên, khi ánh sáng truyền từ chất này sang
chất khác, nó sẽ truyền thẳng đi mà không có sự thay đổi hướng khi nó trực giao
với ranh giới giữa hai chất. Ví dụ, một chùm ánh sáng chạm tới tấm thủy tinh
dày theo phương thẳng đứng sẽ không bị
khúc xạ.
 |
| Ánh sáng đi thẳng khi truyền xiên góc qua mặt phân cách giữa 2 môi trường |
Chùm tia sáng xuất phát tới mặt phân cách giữa hai môi trường gọi là chùm tia tới ( incident ray), chùm tia sáng bị đổi phương khi qua mặt phân cách giữa hai môi trường gọi là chùm tia khúc xạ ( refracted ray), mặt phân cách giữa hai môi trường là mặt lưỡng chất, hệ hai môi trường truyền sáng phân cách bằng mặt phẳng gọi là lưỡng chất phẳng.
Chúng ta chỉ nghiên cứu hiện tượng khúc xạ ở mặt phân cách là phẳng và cũng cần lưu ý cho học sinh rằng bên cạnh hiện tượng khúc xạ vẫn còn hiện tượng phản xạ nếu mặt phân cách là phẳng. hai hiện tượng này xảy ra đồng thời khi một tia sáng đập vào mặt phân cách giữa hai môi trường. Cường độ sáng của hai tia này khác nhau và thay đổi theo góc tới, nhưng sự phân chia năng lượng giữa chúng vẫn tuân theo định luật bảo toàn năng lượng. Để minh họa cho điều này, hãy xem sự mô phỏng sau:
http://phet.colorado.edu/vi/simulation/bending-light
I.2 Quy luật của hiện tượng khúc xạ ánh sáng
Từ thí nghiệm trên ta rút ra định luật khúc xạ ánh sáng có nội dung:
· Tia khúc xạ nằm trong mặt phẳng tới
· Tia tới và tia khúc xạ nằm ở hai bên pháp tuyến tại điểm tới Đối với hai môi trường trong suốt nhất định, tỉ số giữa sin góc tới và sin góc khúc xạ là một hằng số:
Hằng số n ở trên tùy thuộc vào môi trường khúc xạ (môi trường chứa tia khúc xạ) và môi trường tới (môi trường chứa tia tới).
+ Nếu n > 1 ( môi trường khúc xạ chiết quang hơn môi trường tới) thì sini > sinr hay i > r. Trong trường hợp này, khi đi qua mặt lưỡng chất,tia khúc xạ ánh sáng đi gần pháp tuyến hơn tia tới .
+ Nếu n < 1 ( môi trường khúc xạ chiết quang kém hơn môi trương tới ) thì sini < sinr hay i < r.Trong trường hợp này, khi đi qua mặt lưỡng chất, tia sáng đi xa pháp tuyến hơn tia tới.

I.3.1 Vài nét lịch sử

I.2 Quy luật của hiện tượng khúc xạ ánh sáng
I.2.1 Vài nét lịch sử
Để nghiên cứu hiện tượng khúc xạ về mặt định lượng, nhà thiên văn và địa lí Hy Lạp cổ đại Ptolemy đã cố gắng giải thích bằng toán học lượng bẻ cong (khúc xạ) xảy ra, nhưng quy luật mà ông đề xuất sau này được xác định là không xác thực.
Nhà toán học Arập Alhazen cũng đã đưa ra một lý thuyết về khúc xạ ánh sáng vào năm 1000, nhưng không phải bằng ngôn ngữ toán học. Tuy nhiên, trực giác của ông đã tỏ ra đúng đắn. Ông đã cho ánh sáng một vận tốc hữu hạn và thừa nhận ra rằng vận tốc ánh sáng phụ thuộc vào môi trường mà nó đi qua . Alhazen tách vận tốc ánh sáng làm hai thành phần: một vuông góc với mặt phân cách giữa hai môi trường trong suốt, chẳng hạn không khí và nước, và một song song với mặt phân cách ấy; ông nghĩ rằng thành phần song song của tia sáng chậm hơn thành phần nằm vuông góc khi ánh sáng đi vào một môi trường chiết quang hơn (như từ không khí vào nước), làm cho ánh sáng bị lệch về phía pháp tuyến của của mặt phân cách. Ông đã nghiên cứu và thấy được hai góc khúc xạ và góc tới có quan hệ nhưng không xác định được giữa chúng có quan hệ như thế nào.
Trong những năm 1600, nhà toán học người Hà Lan Willebrord Snell đã thành công trong việc phát triển một quy luật định nghĩa một giá trị liên hệ với tỉ số của góc tới và góc khúc xạ, sau này được gọi là sức bẻ cong hay chiết suất của chất. Trong thực tế, một chất càng có khả năng bẻ cong hay làm khúc xạ ánh sáng, người ta nói nó có chiết suất càng lớn. Cái que trong nước trông có vẻ bị bẻ cong vì các tia sáng xuất phát từ que bị bẻ cong đột ngột tại mặt phân giới nước-không khí trước khi đi tới mắt chúng ta. Với tâm trạng chán ngán, Snell chưa bao giờ phát hiện được nguyên nhân cho hiệu ứng khúc xạ này và ông đã không công bố kết qủa của mình.
Sau đó, năm 1937 Descartes cũng đã độc lập tìm ra rằng tỉ số sin góc tới và góc khúc xạ là một hắng số như Snell đã tìm ra. Tuy Snell là người đầu tiên tìm ra định luât khúc xạ nhưng Descartes lại là người đầu tiên công bố nó.
I.2.2 Định luật khúc xạ ánh sáng( ĐL Snen – Đề-các)
Tiến hành thí nghiệm1 : Chiếu một chùm tia sáng song song hẹp SI (coi như một tia sáng) vào mặt phân cách giữa không khí và nước, đựng trong một bể nhỏ có thành bằng thuỷ tinh phẳng, thẳng đứng. Tia tới SI nghiêng trên mặt phân cách. Ta sẽ thấy có một phần chùm tia sáng đi xuyên vào trong nước; nhưng tại điểm tới I, tia sáng bị gẫy khúc. Trong thí nghiệm trên, ta đặt bảng gỗ vuông góc với mặt nước và thay đổi góc tới sao cho tia tới SI quét là là mặt bảng. Ta sẽ thấy tia khúc xạ IK cũng quét là là mặt bảng đó. Như vậy, tia khúc xạ và tia tới luôn luôn nằm trong cùng một mặt phẳng vuông góc với mặt phân cách. Mặt phẳng này chính là mặt phẳng tới. Nó chứa tia tới SI và pháp tuyến IN của mặt phân cách ở điểm tới.
Tiến hành thí nghiệm 2: Trên một tấm kính mờ, đặt một bản trụ D bằng chất rắn trong suốt, ví dụ bằng thủy tinh. Trên tấm kính có một vòng tròn chia độ C . Chiếu mội tia sáng SI (tới điểm I là tâm của bán trụ) là là trên mặt phẳng tấm kính , đường đi của ánh sáng có thể quan sát trên mặt phẳng này.
Quan sát thí nghiệm sẽ cho thấy có tia khúc xạ đi trong bán trụ thủy tinh.
Gọi tia khúc xạ là IR
NN’ là pháp tuyến tại I của mặt lưỡng chất
Góc (SIN) được gọi là góc tới i.Góc (RIN’) được gọi là góc khúc xạ r
Mặt phẳng làm bởi tia tới và pháp tuyến gọi là mặt phẳng tới
Thực hiện thí ngiệm nhiều lần với các góc tới khác nhau và đo góc khúc xạ tương ứng. Lập tỉ số giữa sini và sinr thì ta thấy nó gần như không đổi. Sự sai khác giữa các kết quả là rất nhỏ và coa thể bỏ qua do sai số của phép đo.
Thí nghiệm này đã được người ta thực hiện từ rất xa xưa. Thoạt đầu, người ta tưởng rằng góc khúc xạ tỉ lệ với góc tới. Tuy nhiên, thực nghiệm cho thấy điều này chỉ đúng đối với những góc tới nhỏ và hoàn toàn sai khi góc tới lớn. Mãi đến năm 1621, Snen (người Hà Lan) bằng thực nghiệm mới phát hiện ra là sin của góc khúc xạ tỉ lệ với sin của góc tới. Sau đó ít lâu, Đề-các (người pháp) đã chứng minh kết quả này bằng lý thuyết và phát biểu nó dưới dạng một định luật.
Từ thí nghiệm trên ta rút ra định luật khúc xạ ánh sáng có nội dung:
· Tia khúc xạ nằm trong mặt phẳng tới
· Tia tới và tia khúc xạ nằm ở hai bên pháp tuyến tại điểm tới Đối với hai môi trường trong suốt nhất định, tỉ số giữa sin góc tới và sin góc khúc xạ là một hằng số:
Hằng số n ở trên tùy thuộc vào môi trường khúc xạ (môi trường chứa tia khúc xạ) và môi trường tới (môi trường chứa tia tới).
+ Nếu n > 1 ( môi trường khúc xạ chiết quang hơn môi trường tới) thì sini > sinr hay i > r. Trong trường hợp này, khi đi qua mặt lưỡng chất,tia khúc xạ ánh sáng đi gần pháp tuyến hơn tia tới .
+ Nếu n < 1 ( môi trường khúc xạ chiết quang kém hơn môi trương tới ) thì sini < sinr hay i < r.Trong trường hợp này, khi đi qua mặt lưỡng chất, tia sáng đi xa pháp tuyến hơn tia tới.

Như vậy, sự khúc xạ của tia sáng khi đi qua mặt phân cách giữa hai môi trường phụ thuộc vào môi trường khúc xạ chiết quang hơn hay kém so với môi trường tới. Khi môi trường khúc xạ chiết quang hơn môi trường tới thì tia sáng bị khúc xạ càng mạnh nên đi gần pháp tuyến hơn tia tới. Khi môi trường khúc xạ chiết quang kém môi trường tới thì tia sáng bị khúc xạ càng yếu nên đi xa pháp tuyến hơn tia tới.
I.3 Chiết suất của môi trường I.3.1 Vài nét lịch sử
Khi phát hiện ra tỉ số giữa sin góc tới và góc khúc xạ là một hằng số, Snell đã đóng góp thành công trong việc phát triển một quy luật định nghĩa một giá trị liên hệ với tỉ số của góc tới và góc khúc xạ, sau này được gọi là sức bẻ cong hay chiết suất của chất. Trong thực tế, một chất càng có khả năng bẻ cong hay làm khúc xạ ánh sáng, người ta nói nó có chiết suất càng lớn. Cái que trong nước trông có vẻ bị bẻ cong vì các tia sáng xuất phát từ que bị bẻ cong đột ngột tại mặt phân giới nước-không khí trước khi đi tới mắt chúng ta.
Năm 1678, một nhà khoa học người Hà Lan, Christian Huygens, đã nêu ra một mối quan hệ toán học để giải thích các quan trắc của Snell và cho rằng chiết suất của một chất liên quan tới tốc độ của ánh sáng truyền qua chất đó. Huygens xác định được tỉ số liên hệ giữa góc của các đường đi ánh sáng trong hai chất có chiết suất khác nhau phải bằng với tỉ số vận tốc ánh sáng khi truyền qua mỗi chất đó. Như vậy, ông cho rằng ánh sáng truyền đi chậm hơn trong chất có chiết suất lớn hơn. Phát biểu cách khác, vận tốc ánh sáng qua một môi trường tỉ lệ nghịch với chiết suất của nó. Mặc dù quan điểm này đã được xác nhận bằng thực nghiệm kể từ thời đó, nhưng nó không hiển nhiên ngay đối với đa số các nhà nghiên cứu thế kỉ 17 và 18, những người không có đủ phương tiện đo vận tốc ánh sáng. Đối với những nhà khoa học này, ánh sáng hình như truyền đi ở cùng một tốc độ, không kể vật chất mà nó truyền trong đó là gì. Hơn 150 năm sau khi Huygens qua đời, tốc độ ánh sáng mới được đo chính xác để khẳng định lí thuyết của ông là đúng.

I.3.2 Chiết suất của môi trường
a) Chiết suất tỉ đối
Hiện tượng khúc xạ ánh sáng gây ra do vận tốc truyền song của ánh sáng khác nhau trong các môi trường khác nhau. Bằng nguyên lý Huyghen người ta giải thích khi đập vào mặt phân cách vì vận tốc truyền khác nhau nên mặt đầu song đổi phương do đó phương truyền của tia sáng bị gãy khúc tại mặt phân cách. Trong biểu thức định luật khúc xạ, n được gọi là chiết suất tỉ đối của môi trường khúc xạ đối với môi trường tới .
Khi cho một giá trị chiết suất tỉ đối thì ta phải hiểu đó là chiết suất tỉ đối của môi trường khúc xạ nào đối với môi trường tới nào.
Theo trong lý thuyết sóng ánh sáng, chiết suất tỉ đối này bằng tỉ số giữa các tốc độ của ánh sáng khi đi trong môi trường 1 - môi trường tới và môi trường 2 - môi trường khúc xạ:
Như vậy, chiết suất tỉ đối của môi trường 2 đối với môi trường 1 phụ thuộc vào tốc độ của ánh sáng khi đi trong hai môi trường đó. Khi tốc độ của ánh sáng khi đi trong môi trường 2 lớn hơn tốc độ của ánh sáng khi đi trong môi trường 1 thì tia khúc xạ đi xa pháp tuyến hơn tia tới. Khi tốc độ của ánh sáng khi đi trong môi trường 2 bé hơn tốc độ của ánh sáng khi đi trong môi trường 1 thì tia khúc xạ đi gần pháp tuyến hơn tia tới.
Từ biểu thức của định luật khúc xạ ta đã rút ra được rằng: khi môi trường khúc xạ chiết quang hơn môi trường tới thì tia sáng bị khúc xạ càng mạnh nên đi gần pháp tuyến hơn tia tới. Khi môi trường khúc xạ chiết quang kém môi trường tới thì tia sáng bị khúc xạ càng yếu nên đi xa pháp tuyến hơn tia tới. Như thế, ý nghĩa của chiết suất tỉ đối giữa hai môi trường là khi chiết suất tỉ đối giữa hai môi trường càng lớn thì tia sáng đi qua mặt phân cách giữa hai môi trường bị khúc xạ càng nhiều.
b) Chiết suất tuyệt đối
Khái niệm chiết suất tuyệt đối được định nghĩa dựa trên khái niệm chiết suất tỉ đối của môi trường 2 đối với môi trường 1.
Chiết suất tuyệt đối của một môi trường là chiết suất tỉ đối của môi trường đó đối với chân không. Vì tốc độ ánh sáng truyền trong chân không là c = 300.000 km/s nên từ định nghĩa này,chiết suất tuyệt đối của môi trường 1 và chiết suất tuyệt đối của môi trường 2 lần lượt là:
Từ đó suy ra chiết suất tỉ đối của môi trường 2 đối với môt trường 1 liên hệ với chiết suất tuyệt đối của từng môi trường như sau:
Nếu đặt i =i1,r=i2. Định luật khúc xạ có thể viết lại ở dạng đối xứng:
Từ đây khi nói chiết suất của môi trường là n thì ta hiểu đó là chiết suất tuyệt đối của một môi trường, còn khi nói chiết suất tỉ đối thì phải nói rõ là chiết suất tỉ đối của môi trường 2(môi trường khúc xạ nào) đối với môi trường 1(môi trường tới) nào.
Mọi chiết suất tuyệt đối của một môi trường đều lớn hơn 1 vì tốc độ ánh sáng truyền trong các môi trường bao giờ cũng nhỏ hơn tốc độ ánh sáng trong chân không.
I.4 Ảnh của một vật được tạo bởi sự khúc xạ ánh sáng qua mặt phân cách hai môi trường
Một trong những hiện tượng phổ biến nhất là kinh nghiệm mà nhiều người đã từng trải qua khi cố gắng tiến sát tới và chạm tay vào một vật gì đó chìm trong nước nhưng vật nằm trong nước lại luôn trông có vẻ có chiều sâu khác với chiều sâu thật sự của nó. Hiện tượng này được minh họa tỉ mỉ bởi ảo giác, tạo ra bằng hiện tượng khúc xạ. Chẳng hạn như khi chúng ta nhìn xuyên qua nước để quan sát cá lội xung quanh bể, chúng hình như ở gần mặt nước hơn so với thực tế.
Xét điểm O nằm ở đáy 1 cốc nước. Ta chú ý 2 tia OA, OB; OA vuông góc với mặt nước, B rất gần A. Nếu kéo dài các tia của chùm khúc xạ thì các đường kéo dài gặp nhau tại O’. O’ là điểm ảnh ảo của O. Đặt mắt ngoài không khí sao cho chùm khúc xạ nói trên đi vào mắt, ta sẽ có cảm giác là đáy cốc như được nâng lên cao hơn so với bình thường.

Ta chỉ xét với trường hợp B gần với A tức là chỉ xét trường hợp nhìn theo phương gần như vuông góc với mặt nước.
Ngoài các hiện tượng trên trong thực tế ta còn gặp nhiều hiện tượng khác liên quan đến hiện tượng khúc xạ ánh sáng dưới đây:
- Mặt trời lặn muộn hơn so với thực tế và sự “nhấp nháy” của các ngôi sao
Tương tự, hiện tượng khúc xạ ánh sáng lại “dối gạt” chúng ta thấy rằng Mặt Trời lặn muộn hơn một vài phút so với thực tế nó đã lặn. Đó là do sự thay đổi chiết suất khi ánh sáng truyền từ mặt trời đến bầu khí quyển trái đất.
Khi quan sát một ngôi sao ta thấy nó luôn nhấp nháy và không ở nguyên một vị trí. Khúc xạ ánh sáng cũng là nguyên nhân gây ra hiện tượng này. Chiết suất của môi trường thay đổi theo nhiệt độ và chiết suất này không đồng nhất trong khoảng môi trường từ ngôi sao mà ta quan sát đến mắt chúng ta. Chính vì điều này sẽ làm phát sinh một số điểm ảnh ảo liên tục khác nhau làm cho người quan sát thấy hiện tượng như trên.
- Khúc xạ ánh sáng với thấu kính
Sự khúc xạ ánh sáng khả kiến cũng là một đặc trưng quan trọng ứng dụng trong thấu kính. Thấu kính là tên gọi chung chỉ thành phần thủy tinh hoặc chất liệu plastic trong suốt, thường có dạng tròn, có hai bề mặt chính được mài nhẵn một cách đặc biệt nhằm tạo ra sự hội tụ hoặc phân kì của ánh sáng truyền qua chất đó. Ở một thấu kính lồi đơn giản, sóng ánh sáng phản xạ từ vật thể được thu gom bởi thấu kính và khúc xạ về phía trục chính để hội tụ vào tiêu điểm phía sau. Vị trí tương đối của vật so với tiêu điểm phía trước của thấu kính xác định cách vật được tạo ảnh. Nếu vật nằm phía ngoài khoảng cách hai lần tiêu cự tính từ thấu kính ra thì nó trông nhỏ hơn và bị lộn ngược và phải được tạo ảnh bằng một thấu kính nữa để phóng to kích thước. Tuy nhiên, khi vật ở gần thấu kính hơn so với tiêu điểm phía trước, thì ảnh xuất hiện thẳng đứng và lớn hơn, như có thể dễ dàng chứng minh bằng một cái kính lúp đơn giản.


Hồi đầu thế kỉ 19, những người thợ thêu đã sử dụng những bình cầu thủy tinh rất mỏng chứa nước để hội tụ hoặc tập trung ánh sáng ngọn nến lên khu vực làm việc nhỏ của họ, giúp họ nhìn thấy những chi tiết tinh tế rõ ràng hơn. Hình dưới đây minh họa cái tụ sáng của người thợ thêu hồi những năm 1800, gồm một vài bình cầu thủy tinh sắp xếp thành hình tròn xung quanh một ngọn nến dựng đứng, cho phép ánh sáng phát ra từ ngọn nến hội tụ hoặc tập trung vào một vài đốm sáng. Bề mặt cong của bình cầu thủy tinh đóng vai trò làm bề mặt thu thập các tia sáng, sau đó chúng khúc xạ về phía một tiêu điểm chính theo kiểu tương tự như thấu kính lồi(thấu kính hội tụ).
Thấu kính đơn giản có khả năng tạo ảnh (giống như thấu kính hai mặt lồi) có ích trong những dụng cụ thiết kế dành cho các ứng dụng phóng đại đơn giản, như kính phóng to, kính đeo mắt, camera một thấu kính, kính lúp, ống nhòm và thấu kính tiếp xúc.

Ngoài những dạng hình học phổ biến đã mô tả ở trên, thấu kính cũng được sản xuất thuộc nhiều hình dạng và định hướng khác đa dạng (xem hình 5). Thấu kính hình quả cầu biểu hiện tính chất như nhau từ mọi góc tới, và có tiêu cự phụ thuộc vào đường kính và chiết suất. Bằng cách điều chỉnh hai thông số này, một phổ rộng rãi tiêu cự có thể thu được với thấu kính hình quả cầu nhưng ứng dụng chủ yếu của chúng là cải thiện sự ghép tín hiệu giữa sợi quang, máy phát và máy thu dùng trong công nghiệp viễn thông. Thấu kính hình quả cầu này giống là thấu kính hội tụ và đã sớm được ứng dụng như buổi đầu bởi những người thợ thêu.

Nếu ánh sáng truyền từ S tới R, giả sử theo đường truyền là SIJKR thì khi truyền ngược lại theo tia RK, đường truyền là RKJIS. Như vậy, ánh sáng truyền đi theo đường nào thì cũng truyền ngược lại theo đường đó. Đó là tính thuận nghịch của sự truyền ánh sáng.
Như thế, tính thuận nghịch này biểu hiện ở sự khúc xạ, sự truyền thẳng và sự phản xạ.